问题
解答题
已知函数f(x)=
(1)当a=0时,求f(x)的单调区间; (2)设a>1,若函数f(x)有三个零点,求a的取值范围; (3)若a>-1,求函数|g(x)|在区间[-1,1]内的最大值M(a)的表达式. |
答案
(1)f′(x)=x(x-1),
∴函数f(x)在(-∞,0)及(1,+∞)上单调递增,在(0,1)上单调递减;
(2)f′(x)=(x-a)(x-1),
由f(1)=
a-1 2
>0,f(a)=-1 6
a3+1 6
a2<0,1 2 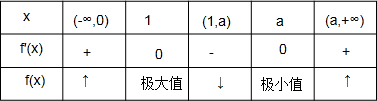
解得a>3;
(3)①当a>1时,|g(x)|在区间[-1,1]内的最大值是g(-1)=2a+2
②当-1<a<1时,0<
<1,|g(x)|在区间[-1,1]内的最大值是a+1 2
max{g(-1),|g(
)|}=max{2a+2,a+1 2
}(a-1)2 4
解不等式2a+2-
>0,得5-4(a-1)2 4
<a<5+42 2
∴当-1<a<5-4
时,|g(x)|在区间[-1,1]内的最大值是2
,(a-1)2 4
当5-4
≤a<1时,|g(x)|在区间[-1,1]内的最大值是2a+2.2
综上M(a)=
.
,-1<a<5-42(a-1)2 4 2a+2,5-42≤a<1
