问题
解答题
求20Cn+55=4(n+4)Cn+3n-1+15An+32中n的值.
答案
n=2
解:20×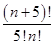 =4(n+4)×
=4(n+4)×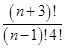 +15(n+3)(n+2)
+15(n+3)(n+2)
即: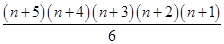
=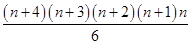 +15(n+3)(n+2)
+15(n+3)(n+2)
∴(n+5)(n+4)(n+1)-(n+4)(n+1)·n=90,
即5(n+4)(n+1)=90,
∴n2+5n-14=0,即n=2或n=-7,
∵n≥1且n∈Z,∴n=2.
求20Cn+55=4(n+4)Cn+3n-1+15An+32中n的值.
n=2
解:20×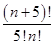 =4(n+4)×
=4(n+4)×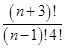 +15(n+3)(n+2)
+15(n+3)(n+2)
即: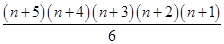
=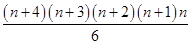 +15(n+3)(n+2)
+15(n+3)(n+2)
∴(n+5)(n+4)(n+1)-(n+4)(n+1)·n=90,
即5(n+4)(n+1)=90,
∴n2+5n-14=0,即n=2或n=-7,
∵n≥1且n∈Z,∴n=2.