问题
解答题
已知二次函数y=mx2+nx+p 图象的顶点横坐标是2 ，与x 轴交于A （x1 ，0 ）、B （x2，0 ），x1＜0＜x2，与y 轴交于点C，O为坐标原点，tan ∠CAO-tan ∠CBO=1。
（1）求证：n+4m=0 ；
（2）求m 、n的值；
（3）当p＞0且二次函数图象与直线y=x+3仅有一个交点时，求二次函数的最大值。
答案
解：（1）将2 代入顶点横坐标得：
∴n+4m=0
（2） ∵已知二次函数图象与x轴交于A（x1，0）、B（x2，0），且由（1）知n=-4m
∴
，
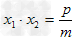
∵ x1<0<x2，
∴在Rt△ACO中，tan∠CAO=
在Rt△CBO中，tan∠CBO=
∵
，
∴
∵x1<0<x2，
∴OC=|p|≠0
∴
即
∴
∴p=-4m|p|
①当p>0时，
，此时，n=1
②当p<0时，
， 此时，n=-1
（3）当p>0时，二次函数的表达式为：
∵二次函数图象与直线y=x+3仅有一个交点
∴方程组
仅有一个解
∴一元二次方程
即
有两个相等根
∴
解得：p=3
此时二次函数的表达式为：
∵
，
∴y有最大值4。