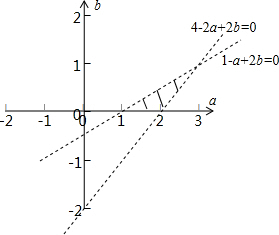由题意，f′（x）=x²+ax+2b．

∵f（x）=

1

3

x³+

1

2

ax²+2bx+c的两个极值点分别是x₁，x₂，x₁∈（-2，-1），x₂∈（-1，0）

∴

f′(-2)=4-2a+2b＞0 f′(-1)=1-a+2b＜0 f′(0)=2b＞0

，

对应的平面区域如图所示，三个顶点坐标为（1，0），（2，0），（3，1），则

在（1，0）处，2a+b2，在（3，1）处，2a+b=7，

∴2a+b的取值范围是（2，7）．

故选B．