问题
解答题
一开口向上抛物线与x轴交于A（m﹣2，0），B（m+2，0）两点，顶点C，且AC⊥BC．
（1）若m为常数，求抛物线解析式．
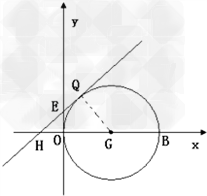
（2）点Q在直线y=kx+1上移动，O为原点，当m=4时，直线上只存在一个点Q使得∠OQB=90°，求此时直线解析式．
答案
解：（1）设抛物线的解析式为：y=a（x﹣m）2﹣2，
∵AC⊥BC，
∴由抛物线的对称性可知：△ACB为等腰直角三角形，
又∵AB=4，
∴B（m+2，0）代入y=a（x﹣m）2﹣2，得a=
．
∴解析式为：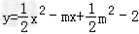
；
（2）当m=4时，B（6，0），y=kx+1与x轴交于H，与y轴交于E（0，1），
设OB中点为G，以OB为直径作⊙G，
当直线与⊙G切于点Q时，只存在一个点Q使∠OQB=90°，
设HO=t，
∵HQ是⊙G切线，
∴∠EOH=HQG=90°，
又∵∠OHE=∠QHG，
∴△HOE∽△HQG，
∴
=
，
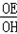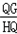由QG=3，OE=1，代入得HQ=3t，
在△HQG中，HQ2+QG2=HG2，即（3t）2+32=（t+3）2，
整理得4t2﹣3t=0，
解得：t=
，或t=0（舍去），
所以点H的坐标为（﹣
，0），
把H（﹣
，0）代入y=kx+1得：k=
，
所以此时直线解析式为y=
x+1．
