问题
解答题
某公司从第1年到第x年的营业收入累计为y万元，且y=6x2+1．
（1）问该公司从第1年到第4年的营业收入累计为多少万元？
（2）该公司平均年支出z（万元）与营业年数x（年）的函数关系式为z=kx+b（k，b为常数，k≠0），若营业1年支出16万元，营业3年的平均年支出为24万元．
①求k与b的值；
②设该公司营业以来获得的总利润为W万元，在营业期间，若该公司的平均年支出不多于68万元，试求W的最大值．（总利润=总收入﹣总支出）
答案
解：（1）x=4时，y=6×42+1=97，
即该公司从第1年到第4年的营业收入累计为97万元；
（2）①把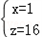
和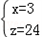
分别代入z=kx+b，
得：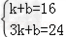
，
解得：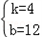
；
②由①得：z=4x+12，
∴4x+12≤68，
解得：x≤14，
∴1≤x≤14，
W=y﹣xz=6x2+1﹣x（4x+12）=2x2﹣12x+1=2（x﹣3）2﹣17．
∵a=2>0，
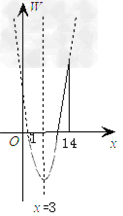
∴函数图象为开口向上的抛物线（如右图），
其对称轴为直线x=3，由函数图象知：
当1≤x≤3时，W随x的增大而减少；
当3<x≤14时，W随x的增大而增大．
而当x=1时，W=﹣9<0，
∴当x=14时，W有最大值，
此时W最大值=2（14﹣3）2﹣17=225（万元）．
