问题
解答题
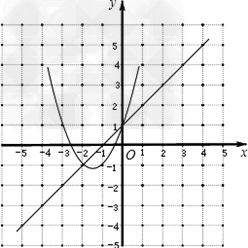
设函数y=kx2+（2k+1）x+1（k为实数）
（1）写出其中的两个特殊函数，使它们的图象不全是抛物线，并在同一直角坐标系中，用描点法画出这两个特殊函数的图象；
（2）根据所画图象，猜想出：对任意实数k，函数的图象都具有的特征，并给予证明；
（3）对任意负实数k，当x＜m时，y随着x的增大而增大，试求出m的一个值．
答案
解：（1）如两个函数为y=x+1，y=x2+3x+1，函数图形如图所示；
（2）不论k取何值，函数y=kx2+（2k+1）x+1的图象必过定点（0，1），（﹣2，﹣1），
且与x轴至少有1个交点．
证明如下：将x=0时代入函数中解出y=1，x=﹣2时代入函数中解出Y=﹣1．
所以函数的图象必过定点（0，1），（﹣2，﹣1）．
又因为当k=0时，函数y=x+1的图象与x轴有一个交点；
当k≠0时，
∵△=（2k+1）2﹣4k=4k2+1＞0，
所以函数图象与x轴有两个交点．
所以函数y=kx2+（2k+1）x+1的图象与x轴至少有1个交点．
（3）只要写出m≤﹣1的数都可以．
∵k＜0，
∴函数y=kx2+（2k+1）x+1的图象在对称轴直线x=﹣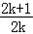
的左侧，
y随x的增大而增大．
根据题意，得m≤﹣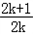
，而当k＜0时，﹣
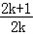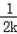=﹣1﹣
＞﹣1，
所以m≤﹣1．
