问题
解答题
将一根长为16π厘米的细铁丝剪成两段．并把每段铁丝围成圆,设所得两圆半径分别为r1和r2
（1）求r1与r2的关系式，并写出r1的取值范围；
（2）将两圆的面积和S表示成r1的函数关系式，求S的最小值．
答案
解：（1）由题意，有2πr1+2πr2=16π，
则r1+r2=8，
∵r1＞0，r2＞0，
∴0＜r1＜8．
即r1与r2的关系式为r1+r2=8，r1的取值范围是0＜r1＜8厘米；
（2）∵r1+r2=8，∴r2=8﹣r1，
又∵S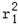=π
+π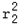
，
∴S=π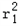
+π（8﹣r1）2=2π
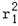﹣16πr1+64π=2π（r1﹣4）2+32π，
∴当r1=4厘米时，S有最小值32π平方厘米．