问题
解答题
已知二次函数的图象经过点(0,3),(﹣3,0),(2,﹣5),且与x轴交于A、B两点.
(1)试确定此二次函数的解析式;
(2)判断点P(﹣2,3)是否在这个二次函数的图象上?如果在,请求出△PAB的面积;如果不在,试说明理由.
答案
解:(1)设二次函数的解析式为y=ax2+bx+c;
∵二次函数的图象经过点(0,3),(﹣3,0),(2,﹣5),
则有: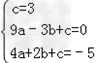 ,
,
解得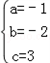 ;
;
∴y=﹣x2﹣2x+3
(2)∵﹣(﹣2)2﹣2×(﹣2)+3=﹣4+4+3=3
∴点P(﹣2,3)在这个二次函数的图象上
∵﹣x2﹣2x+3=0,
∴x1=﹣3,x2=1;
∴与x轴的交点为:(﹣3,0),(1,0)
∴S△PAB= ×4×3=6.
×4×3=6.
