问题
选择题
f(x),g(x)都是定义在R上的单调递增函数,f(x)>0,g(x)<0,则
|
答案
由f(x)>0,g(x)<0得,
<0,f(x) g(x)
设x1<x2,则f(x1)<f(x2),g(x1)<g(x2),
-f(x1) g(x1)
=f(x2) g(x2) f(x1)g(x2)-f(x2)g(x1) g(x1)g(x2)
=f(x1)g(x2)-f(x1)g(x1)+f(x1)g(x1)-f(x2)g(x1) g(x1)g(x2)
=
,f(x1)[g(x2)-g(x1)]+[f(x1)-f(x2)]g(x1) g(x1)g(x2)
因为f(x)>0,g(x)<0,f(x1)<f(x2),g(x1)<g(x2),
所以g(x1)g(x2)>0,f(x1)[g(x2)-g(x1)]>0,[f(x1)-f(x2)]g(x1)>0,
所以
-f(x1) g(x1)
>0,即f(x2) g(x2)
>f(x1) g(x1)
,f(x2) g(x2)
所以
递减,f(x) g(x)
故选B.

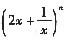 的展开式中第m项的系数为bm,若b3=2b4,则n=______。
的展开式中第m项的系数为bm,若b3=2b4,则n=______。