令f（x）=x²-2ax-2alnx=0，则2a（x+lnx）=x²，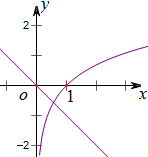

∴2a=

x2

x+lnx

，令g（x）=

x2

x+lnx

，

则g′（x）=

2x(x+lnx)-x2(1+ 1 x )

(x+lnx)2

=

x(x-1+2lnx)

(x+lnx)2

令h（x）=x+lnx，通过作出两个函数y=lnx及y=-x的图象（如右图）发现h（x）有唯一零点在（0，1）上，

设这个零点为x₀，当x∈（0，x₀）时，g′（x）＜0，g（x）在（0，x₀）上单调递减，x=x₀是渐近线，

当x∈（x₀，1）时，g′（x）＜0，则g（x）在（x₀，1）上单调递减，

当x∈（1，+∞）时g′（x）＞0，g（x）在（1，+∞）单调递增，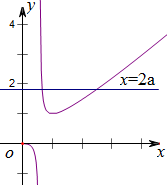

∴g（1）=1，可以作出g（x）=

x2

x+lnx

的大致图象，

结合图象可知，当a＜0时，y=2a与y=g（x）的图象只有一个交点，则函数y=f（x）只有一个零点，故选项A正确；

若函数y=f（x）有零点，则a＜0或a≥

1

2

，故选项B不正确；

存在a=

1

2

＞0，函数y=f（x）有唯一零点，故选项C正确；

若函数y=f（x）有唯一零点，则a＜0，或a=

1

2

，则a≤1，故选项D正确．

故选B．