问题
解答题
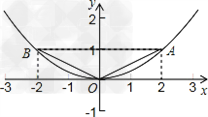
已知抛物线y=ax2经过点A（2，1）
（1）求这个函数的解析式；
（2）写出抛物线上点A关于y轴的对称点B的坐标；
（3）求△OAB的面积；
（4）抛物线上是否存在点C，使△ABC的面积等于△OAB面积的一半？若存在，求出C点的坐标，若不存在，请说明理由．
答案
解：（1）∵抛物线y=ax2经过点A（2，1），
∴4a=1，解得a=
，
∴这个函数的解析式为y=
x2；
（2）∵点A（2，1），
∴点A关于y轴的对称点B的坐标为（﹣2，1）；
（3）∵点A（2，1），B（﹣2，1），
∴AB=2﹣（﹣2）=2+2=4，
S△OAB=
×4×1=2；
（4）假设存在点C，且点C到AB的距离为h， 则S△ABC=
AB﹒h=
×4h，
∵△ABC的面积等于△OAB面积的一半，
∴
×4h=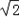
×2，解得h=
，
①当点C在AB下面时，点C的纵坐标为1﹣
=
，
此时，
x2=
，解得x1=
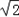，x2=﹣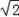
，
点C的坐标为（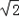
，
）或（﹣，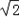
），
②点C在AB的上面时，点C的纵坐标为1+
=
，
此时
x2=
，解得x1=
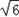，x2=﹣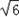
，
点C的坐标为（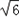
，
）或（﹣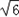
，
），
综上所述，存在点C（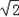
，
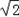）或（﹣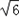
，
）或（
，
）或（﹣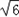
，
），
使△ABC的面积等于△OAB面积的一半．
