问题
填空题
已知函数f(x)=x3+bx2+cx+d的区间[-1,2]上是减函数,则b+c的取值范围是______.
答案
由f(x)=x3+bx2+cx+d,
则f′(x)=3x2+2bx+c.
要使函数f(x)=x3+bx2+cx+d的区间[-1,2]上是减函数,
则f′(x)=3x2+2bx+c≤0在x∈[-1,2]上恒成立.
所以
,即f′(-1)≤0 f′(2)≤0
.3×(-1)2-2b+c≤0 3×22+4b+c≤0
也就是
.2b-c≥3 4b+c≤-12
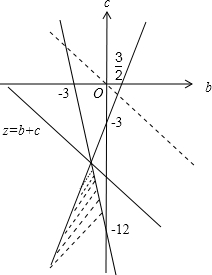
以b为横轴,c为纵轴画出可行域如图,
联立
,解得2b-c=3 4b+c=-12
.b=- 3 2 c=-6
所以可行域上顶点为(-
,-6).3 2
则b+c的最大值为-
-6=-3 2
.15 2
故b+c的取值范围是(-∞,-
].15 2
故答案为(-∞,-
].15 2