问题
解答题
已知函数f（x）=（ax2-2x）e-x（a∈R）．
（1）当a≥0时，求f（x）的极值点；
（2）设f（x）在[-1，1]上是单调函数，求出a的取值范围．
答案
（1）令f′（x）=e-x[-ax2+2（a+1）x-2]=0（a≥0）
当a=0时，解得：x=1
∵x＜1，f'（x）＜0；x＞1，f'（x）＞0
∴x=1时，f（x）取得极小值；
当a＞0时，x1=
，x2=a+1- a2+1 a a+1+ a2+1 a
易得：x1=
＜a+1- a2+1 a
=x2，从而有下表a+1+ a2+1 a
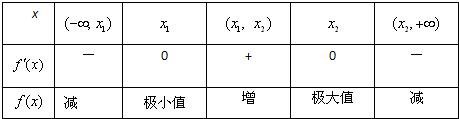
∴x=
是函数的极小值点；x=a+1- a2+1 a
是函数的极大值点．a+1+ a2+1 a
（2）当a=0时，由（1）可知，函数在[-1，1]上单减，符合题意；
当a＞0时，若函数在[-1，1]上单增，则
解得：a∈ϕ
≤-1a+1- 1+a2 a
≥1a+1+ 1+a2 a
若函数在[-1，1]上单减，则
≥1；或a+1- a2+1 a
≤-1a+1+ a2+1 a
解得：a∈ϕ
当a＜0时，x1=
＞a+1- a2+1 a
=x2a+1+ a2+1 a
若函数在[-1，1]上单增，则
≤-1；或a+1- a2+1 a
≥1a+1+ a2+1 a
解得：a∈ϕ
若函数在[-1，1]上单减，则
⇒
≤-1a+1+ 1+a2 a
≥1a+1- 1+a2 a -
≤a＜04 3 a∈R
解得：a∈[-
，0)4 3
综合得：a∈[-
，0]时，函数在[-1，1]上是单减函数．4 3
2MgO 
Na2SO4+Cu(OH)2