问题
解答题
已知：二次函数y=-x2+bx+c的图象与x轴交于A，B两点，其中A点坐标为（-3，0），与y轴交于点C，点D( -2，-3)在抛物线上．
(1)求抛物线的解析式；
(2)抛物线的对称轴上有一动点P，求出PA+ PD的最小值．
答案
解：(1) 将A （－3 ，0 ），D( －2 ，－3) 代人y ＝x2＋bx ＋c 得：
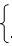
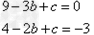解得：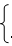
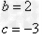
∴抛物线的解析式为：y＝x2＋2x－3．
(2)由：y=x2＋2x－3得： 对称轴为：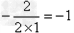
．
令：y=0，则：x2＋2x－3＝0
∴x1＝－3，x2＝1
∴点B坐标为(1，0)
而点A与点B关于y轴对称
∴连接BD与对称轴的交点即为所求的P点，
过点D做DF⊥x轴于点F，则：
DF＝3，BF＝1－（－2）＝3
在Rt△BDF中，BD=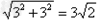
∵PA= PB
∴PA+ PD= PB+ PD= BD =3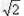
，即PA+ PD的最小值为3
．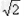