问题
解答题
在产品质量检验时，常从产品中抽出一部分进行检查．现在从98件正品和2件次品共100件产品中，任意抽出3件检查．
(1)共有多少种不同的抽法？
(2)恰好有一件是次品的抽法有多少种？
(3)至少有一件是次品的抽法有多少种？
(4)恰好有一件是次品，再把抽出的3件产品放在展台上，排成一排进行对比展览，共有多少种不同的排法？
答案
（1）161700 （2）9506 （3）9604 （4）57036
解：(1)所求不同的抽法数，即从100个不同元素中任取3个元素的组合数，共有C1003＝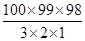
＝161700(种)．
(2)抽出的3件中恰好有一件是次品这件事，可以分两步完成：
第一步，从2件次品中任取1件，有C21种方法；
第二步，从98件正品中任取2件，有C982种方法．
根据分步计数原理，不同的抽取方法共有
C21·C982＝2×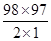
＝9506(种)．
(3)法一 抽出的3件中至少有一件是次品这件事，分为两类：
第一类：抽出的3件中有1件是次品的抽法，有C21C982种；
第二类：抽出的3件中有2件是次品的抽法，有C21C981种．
根据分类计数原理，不同的抽法共有
C21·C982＋C22·C981＝9506＋98＝9604(种)．
法二 从100件产品中任取3件的抽法，有C1003种，其中抽出的3件中没有次品的抽法，有C983种．所以抽出的3件中至少有一件是次品的抽法，共有C1003－C983＝9604(种)．
(4)完成题目中的事，可以分成两步：
第一步，选取产品，有C21C982种方法；
第二步，选出的3个产品排列，有A33种方法．
根据分步计数原理，不同的排列法共有
C21C982A33＝57036(种)．