问题
解答题
某种商品以8元购进，若按每件10元售出，每天可销售200件，现采用提高售价，减少进货量的办法来增加利润，已知这种商品每涨价0.5元，其销售量就减少10件．
（1）当售价提高多少元时，每天利润为700元？
（2）设售价为x元，利润为y元，请你探究售价为多少元时，利润最大，最大利润是多少？
答案
解：设应将售价提为x元时，才能使得所赚的利润最大为y元，
根据题意得：y=（x﹣8）（200﹣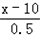
×10）=﹣20x2+560x﹣3200，
令y=700，即﹣20x2+560x﹣3200=700，
解得x=13或15，
故当售价提高13或15元时，每天利润为700元；
（2）化简配方y=（x﹣8）（20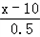0﹣
×10），
=﹣20x2+560x﹣3200，
=﹣20（x2﹣28x）﹣3200，
=﹣20（x﹣14）2+720，
∴x=14时，利润最大y=720．
答：应将售价提为14元时，才能使所赚利润最大，最大利润为720元．