问题
问答题
在倾角为θ的长斜面上有一带风帆的滑块从静止开始沿斜面下滑,滑块的质量为m,它与斜面间的动摩擦因数为μ,帆受到的空气阻力方向沿斜面且大小与滑块下滑的速度大小成正比,即Ff=kv.
(1)写出滑块下滑速度为v时加速度的表达式;
(2)写出滑块下滑的最大速度的表达式;
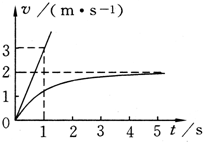
(3)若m=2kg,θ=30°,g取10m/s2,滑块从静止开始沿斜面下滑的速度图线如图所示,图中直线是t=0时刻速度图线的切线.求μ和k的值.
答案
(1)滑块在斜面上受到重力、支持力、摩擦力和空气阻力作用做加速运动.
根据牛顿第二定律得:
mgsinθ-μmgcosθ-kv=ma
a=gsinθ-μgcosθ-kv m
(2)分析上式,当v增加时,a减小,
当a=0时,v最大
vmax=mg(sinθ-μcosθ) k
(3)图中直线是t=0时刻速度图线的切线,v-t图象中斜率代表加速度.
从v-t图可以得出vmax=2m/s
当t=0、v=0时,a=3m/s2
所以得:
10sin30°-μ×10cos30°=3
2=
(sin30°-μcos30°)2×10 k
解得:μ=
,k=3N•s/m.2 3 15
答:(1)滑块下滑速度为v时加速度的表达式是gsinθ-μgcosθ-
;kv m
(2)滑块下滑的最大速度的表达式是
;mg(sinθ-μcosθ) k
(3)μ=
,k=3N•s/m.2 3 15
