（1）f'（x）=-

ax2+2x-1

x

（x＞0）

依题意f'（x）≥0 在x＞0时恒成立，即ax²+2x-1≤0在x＞0恒成立．

则a≤

1-2x

x2

=在x＞0恒成立，

即a≤[(

1

x

-1)2-1]min x＞0

当x=1时，(

1

x

-1)2-1取最小值-1

∴a的取值范围是（-∝，-1]

（2）a=-

1

2

，f（x）=-

1

2

x+b∴

1

4

x2-

3

2

x+lnx-b=0

设g（x）=

1

4

x2-

3

2

x+lnx-b(x＞0)则g'（x）=

(x-2)(x-1)

2x

列表：

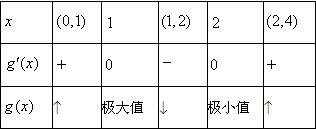
∴g（x）极小值=g（2）=ln2-b-2，g（x）极大值=g（1）=-b-

5

4

，

又g（4）=2ln2-b-2

∵方程g（x）=0在[1，4]上恰有两个不相等的实数根．

则

g(1)≥0 g(2)＜0 g(4)≥0

，得ln2-2＜b≤-

5

4

．