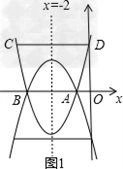
已知：抛物线y=ax2+4ax+t与x轴的一个交点为A（﹣1，0）。
（1）求抛物线与x轴的另一个交点B的坐标；
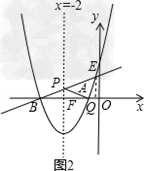
（2）D是抛物线与y轴的交点，C是抛物线上的一点，且以AB为一底的梯形ABCD的面积为9，求此抛物线的解析式；（3）E是第二象限内到x轴、y轴的距离的比为5：2的点，如果点E在（2）中的抛物线上，且它与点A在此抛物线对称轴的同侧，问：在抛物线的对称轴上是否存在点P，使△APE的周长最小？若存在，求出点P的坐标；若不存在，请说明理由。
解：（1）依题意，抛物线的对称轴为x=﹣2，
∵抛物线与x轴的一个交点为A（﹣1，0），
∴由抛物线的对称性，可得抛物线与x轴的另一个交点B的坐标为（﹣3，0）；
（2）∵抛物线y=ax2+4ax+t与x轴的一个交点为A（﹣1，0）
∴a（﹣1）2+4a（﹣1）+t=0
∴t=3a
∴y=ax2+4ax+3a
∴D（0，3a）
∴梯形ABCD中，AB∥CD，且点C在抛物线y=ax2+4ax+3a上，
∵C（﹣4，3a）
∴AB=2，CD=4
∵梯形ABCD的面积为9
∴
（AB+CD）·OD=9
∴
（2+4）|3a|=
（AB+CD）·OD=9
∴a±1
∴所求抛物线的解析式为y=x2+4x+3或y=﹣x2﹣4x﹣3；
（3）设点E坐标为（x0，y0），依题意，x0＜0，y0＞0，且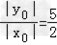
∴y0=﹣
x0
①设点E在抛物线y=x2+4x+3上，
∴y0=x02+4x0+3
解方程组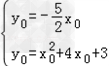
得
，
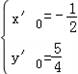
∵点E与点A在对称轴x=﹣2的同侧
∴点E坐标为（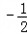
，
），
设在抛物线的对称轴x=﹣2上存在一点P，使△APE的周长最小，
∵AE长为定值，
∴要使△APE的周长最小，只须PA+PE最小
∴点A关于对称轴x=﹣2的对称点是B（﹣3，0）
∴由几何知识可知，P是直线BE与对称轴x=﹣2的交点
设过点E、B的直线的解析式为y=mx+n
∴
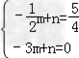，解得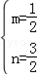
∴直线BE的解析式为y=
x+
∴把x=﹣2代入上式，得y=
∴点P坐标为（﹣2，
）
②设点E在抛物线y=﹣x2﹣4x﹣3上
∴y0=﹣x02﹣4x0﹣3，
解方程组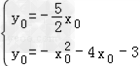
消去y0，
得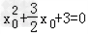
∴△＜0
∴此方程无实数根，
综上，在抛物线的对称轴上存在点P（﹣2，
），使△APE的周长最小。
