问题
解答题
已知圆锥的底面半径为r，高为h，正方体ABCD-A′B′C′D′内接于圆锥，求这个正方体的棱长．
答案
解：设正方体棱长为a，
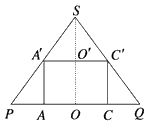
如右图作出组合体的轴截面，
则OS=h，OP=r，OA=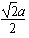
，
∵△SO′A′∽△SOP，
∴
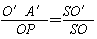，即
，
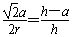∴a=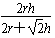
，即正方体的棱长为
。
搜题请搜索小程序“爱下问搜题”
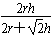已知圆锥的底面半径为r，高为h，正方体ABCD-A′B′C′D′内接于圆锥，求这个正方体的棱长．
解：设正方体棱长为a，
如右图作出组合体的轴截面，
则OS=h，OP=r，OA=，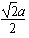
∵△SO′A′∽△SOP，
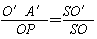∴，即，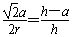
∴a=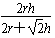，即正方体的棱长为。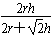