（1）当a=1时，f（x）=lnx-x-3，（x＞0），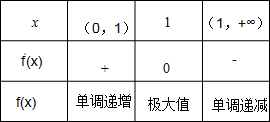

∴f′(x)=

1

x

-1=

1-x

x

，令f^′（x）=0，则x=1．

列表如下：

由表可知：f（x）在（0，1）上单调递增；在（1，+∞）上单调递减．

（2）当a=2时，f（x）=2lnx-2x-3．

令F（x）=h（x）-f（x）=（p-2）x-

p+2e

x

-3-（2lnx-2x-3）=px-

p

x

-2lnx-

2e

x

．

①当p≤0时，px-

p

x

=p

x2-1

x

≤0，

-2e

x

-2lnx＜0，

∴在[1，e]上不存在x₀满足F（x）＞0，即h（x₀）＞f（x₀）不成立．

②当p＞0时，F^′（x）=

px2+p+2e-2x

x2

，

∵x∈[1，e]，∴2e-2p≥0，∴F^′（x）＞0在[1，e]上恒成立，故F（x）在[1，e]上单调递增．

∴F（x）_max=F（e）=pe-

p

e

-4．

故只要pe-

p

e

-4＞0，解得p＞

4e

e2-1

．

所以P的取值范围是(

4e

e2-1

，+∞)．