问题
解答题
如图，抛物线y=﹣x2+bx+c与x轴的两个交点分别为A（1，0），B（3，0）。
（1）求这条抛物线对应函数的表达式；
（2）若P点在该抛物线上，求当△PAB的面积为8时，点P的坐标。
答案
解：（1）点（1，0），（3，0）
在抛物线y=﹣x2+bx+c上，
则有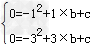
解得：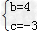
则所求表达式为y=﹣x2+4x﹣3；
（2）依题意，得AB=3﹣1=2，
设P点坐标为（a，b）
当b＞0时，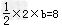
，则b=8，
故﹣x2+4x﹣3=8
即x2+4x+11=0
△=（﹣4）2﹣4×1×11=16﹣44=﹣28＜0，
方程﹣x2+4x+11=0无实数根，
当b＜0时，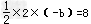
，
则b=﹣8
故﹣x2+4x﹣3=﹣8
即﹣x2+4x﹣5=0
解得x1=﹣1，x2=5
所求点P坐标为（﹣1，﹣8），（5，﹣8）。