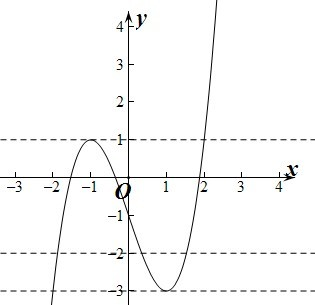问题
填空题
已知函数f(x)=x3-3ax-1,a≠0.若f(x)在x=-1处取得极值,直线y=m与y=f(x)的图象有三个不同的交点,则m的取值范围是______.
答案
函数的导数为f'(x)=3x2-3a,因为f(x)在x=-1处取得极值,
所以f'(-1)=0,即3-3a=0,解得a=1.
所以f(x)=x3-3x-1,f'(x)=3x2-3=3(x2-1)=3(x-1)(x+1),
当f'(x)>0,得x>1或x<-1.当f'(x)<0,得-1<x<1.
即函数在x=-1处取得极大值f(-1)=1,在x=1处取得极小值f(1)=-3,
要使直线y=m与y=f(x)的图象有三个不同的交点,则m小于极大值,大于极小值,
即-3<m<1,所以m的取值范围是(-3,1).
故答案为:(-3,1).