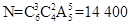(1)； (2)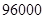

题目分析：(1)本题中不仅要选出5名医生（元素），还要求分配到5个地区（空位），因此是一道“既选又排”的排列组合综合问题，解决这类问题的方法是“先选后排”，同时要注意特殊元素、特殊位置优先安排的原则。

（2）首先将分成以下两类情况第一类：一组中女医生1人，男医生4人，另一组中女医生3人，男医生2人；第二类：两组中人数都有女医生2人男医生3人；最后将这两组医生分派到两地去，并且每组选出正副组长两人，是排列问题．

(1)分三步完成．

第一步：从6名男医生中选3名有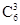种方法；

第二步：从4名女医生中选2名有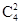种方法；

第三步：对选出的5人分配到5个地区有A种方法．

根据分步乘法计数原理，共有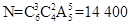(种)．

(2)医生的选法有以下两类情况：

第一类：一组中女医生1人，男医生4人，另一组中女医生3人，男医生2人．共有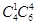种不同的分法；

第二类：两组中人数都有女医生2人男医生3人．因为组与组之间无顺序，故共有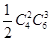种不同的分法．

因此，把10名医生分成两组，每组5人且每组都要有女医生的不同的分法共有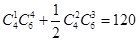种．

若将这两组医生分派到两地去，并且每组选出正副组长两人，则共有

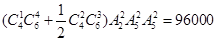种不同方案