问题
解答题
在△OAB中,O为坐标原点,横、纵轴的单位长度相同,A、B的坐标分别为(8,6),(16,0),点P沿OA边从点O开始向终点A运动,速度每秒1个单位,点Q沿BO边从B点开始向终点O运动,速度每秒2个单位,如果P、Q同时出发,用t(秒)表示移动时间,当这两点中有一点到达自己的终点时,另一点也停止运动。
求:(1)几秒时PQ∥AB;
(2)设△OPQ的面积为y,求y与t的函数关系式;
(3)△OPQ与△OAB能否相似,若能,求出点P的坐标,若不能,试说明理由。
答案
(1)由已知得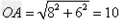 ,当PQ∥AB时
,当PQ∥AB时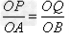 ,则:
,则: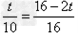 ,
,
得: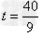
(2) 过P作PC⊥OB, 垂足为C, 过A作AD⊥OB, 垂足为D
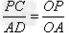 ,
,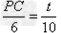
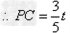

(3)能相似。PQ∥AB, △OPQ∽△OAB
∵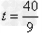 ∴OP
∴OP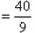 ,
,
∵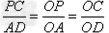
其中AD = 6,OA =10,OD = 8
∴OC = 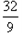 ,PC =
,PC = 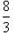 ,
,
∴P点坐标是(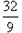 ,
,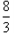 ).
).
