问题
解答题
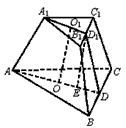
已知正三棱台的侧面和下底面所成的二面角为60°，棱台下底面的边长为a，侧面积为S，求棱台上底面的边长．
答案
解：设O，O1分别为下，上底面中心，连接OO1，
则OO1⊥平面ABC，
上底面边长为x，连接AO，A1O1并延长交BC，B1C1分别于D、D1两点，
则AD⊥BC，
连接DD1，则DD1⊥BC，
∠ADD1为二面角A-BC-D1的平面角，即∠ADD1=60°，
过D1作D1E∥OO1交AD于E，则D1E⊥平面ABC，
在正△ABC，△A1B1C1中，AD=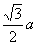
，A1D1=
，
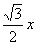在Rt△D1ED中，ED=OD-OE=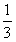
（AD-A1D1）=
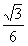（a-x），
则D1D=2ED=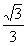
（a-x），
由题意S=3·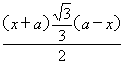
，即S=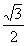
（a2-x2），
解得：x=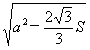
。
问答题