已知函数f（x）=（-x2+ax+b）e-x，a∈R （1）若b=-a，求y=f

问题解答题

已知函数f（x）=（-x²+ax+b）e^-x，a∈R

（1）若b=-a，求y=f（x）的单调区间；

（2）若b=0，且f（x）在（-1，1）上单调递减，求a的取值范围．

答案

（1）当b=-a时，函数f（x）=（-x²+ax-a）e^-x，∴f^′（x）=[x²-（2+a）x+2a]e^-x=（x-a）（x-2）e^-x，令f^′（x）=0，则x=2或a．

①当a=2时，f^′（x）=（x-2）²e^-x≥0，因此f（x）在R上单调递增；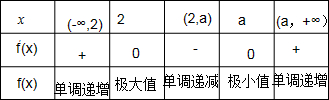

②当a＞2时，如表所示，函数在区间（-∞，2），（a，+∞）上单调递增；在区间（2，a）上单调递减；

③同理：当a＜2时，函数在区间（-∞，a），（2，+∞）上单调递增；在区间（a，2）上单调递减．

（2）b=0，f（x）=（-x²+ax）e^-x，∴f^′（x）=[x²-（a+2）x+a]e^-x．

∵f（x）在（-1，1）上单调递减，∴f^′（x）≤0，∴x²-（a+2）x+a≤0在（-1，1）上单调递减，

∴

f(-1)≤0

f(1)≤0

，解得a≤-

．

因此a的取值范围为(-∞，-

]．