问题
多选题
如图所示，两块平行放置的金属板A、B相距为d，开始S是闭合的，两板间的一油滴（质量为m，电量为q）恰处于静止状态（ ）
A．若将A板向左平移一小段，则油滴向下加速运动，G中有由a-＞b的电流
B．若将A板向左平移一小段，则油滴仍静止不动，G中有由b-＞a的电流
C．若将A板向左平移一小段，则油滴向上加速运动，G中有由b-＞a的电流
D．若将S断开，并将A、B板间距离变大，则油滴仍静止，G中无电流
答案
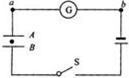
A、B、C电容器保持与电源相连，其电压不变，板间电场强度E=
不变，油滴仍静止不动．将A板向左平移一小段，电容器两极板正对面积减小，电容C减小，由C=U d
分析可知，电量Q减小，电容放电，而电容器下板带正电，放电电流方向为逆时针方向，则G中有由b＞a的电流．故AC错误，B正确．Q U
D、将S断开，电容器的电量不变，G中无电流．将A、B板间距离变大，由推论：板间电场强度E=
，Q、S、ɛ不变，则改变d，E不变，油滴受的电场力不变，仍静止．故D正确．4πkQ ɛS
故选BD．
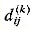为从顶点i到顶点j的一条最短路径的权重。
；当k＞0时，该最短路径上所有的中间顶点均属于集合1，2，…，k。
；若中间顶点不包括顶点k，则
。
给出了任意两个顶点之间的最短路径，即对所有i，j∈V，
表示顶点i到顶点j的最短路径。