（1）f′（x）=3（x2-2），令f′（x）=0，得x=-

2

或

2

，

当 x＜-

2

或x＞

2

时，f′（x）＞0，当-

2

＜x＜

2

时，f′（x）＜0，

∴f（x）的单调递增区间是 （-∞，-

2

）和（

2

，+∞），单调递减区间是 （-

2

，

2

），

当 x=-

2

时，f（x）有极大值5+4

2

；当 x=

2

时，f（x）有极小值5-4

2

，

（2）由（1）可作出y=f（x）图象的大致形状，如下图所示：

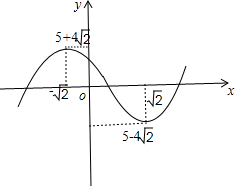
由图象知：当 5-4

2

＜a＜5+4

2

时，直线y=a与y=f（x）的图象有3个不同交点，即方程f（x）=a有三个不同的根．

故实数a的取值范围为：（5-4

2

，5+4

2

）．