问题
解答题
（本题满分12分）
已知f(x)=2x3+ax2+bx+c在x=－1处取得极值8，又x=2时,f(x) 也取得极值。
(1)求a,b,c的值，写出f(x)的解析式；
(2)求f(x)的单调区间。
答案
f(x)=2x3-3x2-12x+1
增区间为:(
,(2,
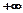) 单调减区间为(-1,2)
解：(1)
,由题意可知,x=-1,x=2是方程6x2+2ax+b=0的两根,故:x1+x2="="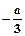 
="1, " ∴a=-3,-2=
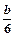, ∴b="-12," 又,当x=-1时f(x)的极值是8,
∴c="1 " ∴f(x)=2x3-3x2-12x+1 (6分)
(2)∵f(x)=6x2-6x-12, 令f(x)="0," 即6x2-6x-12="0, " ∴x=2或x=-1,
解得函数的单调区间为:
增区间为:(,(2,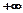) 单调减区间为(-1,2) (6分)