设函数f(x)=(x2+ax+b)ex(x∈R).
(1)若a=2,b=-2,求函数f(x)的极大值;
(2)若x=1是函数f(x)的一个极值点.
①试用a表示b;
②设a>0,函数g(x)=(a2+14)ex+4.若ξ1、ξ2∈[0,4],使得|f(ξ1)-g(ξ2)|<1成立,求a的取值范围.
(1)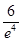 (2)①b=-3-2a②1-
(2)①b=-3-2a②1-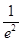 <a<1+
<a<1+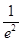 .
.
(1)∵f′(x)=(2x+a)ex+(x2+ax+b)ex=[x2+(2+a)x+(a+b)]ex,
当a=2,b=-2时,f(x)=(x2+2x-2)ex,
则f′(x)=(x2+4x)ex,
令f′(x)=0得(x2+4x)ex=0,
∵ex≠0,∴x2+4x=0,解得x=-4或x=0,
列表如下:
| x | (-∞,-4) | -4 | (-4,0) | 0 | (0,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | 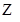 | 极大值 | 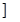 | 极小值 | 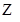 |
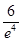 .
.(2)①由(1)知f′(x)=[x2+(2+a)x+(a+b)]ex.
∵x=1是函数f(x)的一个极值点,∴f′(1)=0,
即e[1+(2+a)+(a+b)]=0,解得b=-3-2a.
②由①知f′(x)=ex[x2+(2+a)x+(-3-a)]=ex(x-1)[x+(3+a)],
当a>0时,f(x)在区间(0,1)上的单调递减,在区间(1,4)上单调递增,
∴函数f(x)在区间[0,4]上的最小值为f(1)=-(a+2)e.
∵f(0)=b=-3-2a<0,f(4)=(2a+13)e4>0,
∴函数f(x)在区间[0,4]上的值域是[f(1),f(4)],
即[-(a+2)e,(2a+13)e4].
又g(x)=(a2+14)ex+4在区间[0,4]上是增函数,且它在区间[0,4]上的值域是[(a2+14)e4,(a2+14)e8],
∴(a2+14)e4-(2a+13)e4=(a2-2a+1)e4=(a-1)2e4≥0,
∴存在ξ1、ξ2∈[0,4]使得|f(ξ1)-g(ξ2)|<1成立只须(a2+14)e4-(2a+13)e4<1 (a-1)2e4<1
(a-1)2e4<1 (a-1)2<
(a-1)2<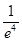
 1-
1-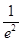 <a<1+
<a<1+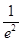 .
.
