（本小题满分14分）
已知函数F(x)=|2x－t|－x3+x+1（x∈R，t为常数，t∈R）.
(Ⅰ)写出此函数F(x)在R上的单调区间；
(Ⅱ)若方程F(x)－k=0恰有两解，求实数k的值．
i) 当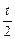
<－1时，F(x)在区间(－∞，－1)上是减函数，
在区间(－1，1)上是增函数，在区间(1，+∞)上是减函数．
ii) 当1>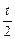≥－1时，F(x)在区间(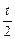－∞，)上是减函数，
在区间(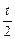，1)上是增函数，在区间(1，+∞)上是减函数．
iii) 当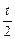≥1时，F(x)在(－∞，+∞)上是减函数．i) 当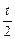<－1时，F(x)在x=－1处取得极小值－1－t，
在x=1处取得极大值3－t，若方程F(x)－m=0恰有两解，
此时m=－1－t或m=3－t．
ii) 当－1≤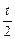<1，F(x)在x=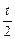处取值为
，
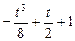在x=1处取得极大值3－t，若方程F(x)－m=0恰有两解，
此时m=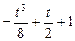或m=3－t．
iii) 当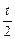≥1时，不存在这样的实数m，使得F(x)－m=0恰有两解
(Ⅰ)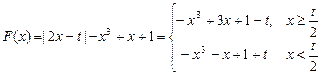
∴
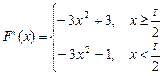.……………..4分
由－3x2+3="0" 得x1=－1，x2=1，而－3x2－1<0恒成立，
∴ i) 当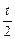<－1时，F(x)在区间(－∞，－1)上是减函数，
在区间(－1，1)上是增函数，在区间(1，+∞)上是减函数．
ii) 当1>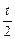≥－1时，F(x)在区间(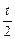－∞，)上是减函数，
在区间(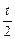，1)上是增函数，在区间(1，+∞)上是减函数．
iii) 当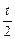≥1时，F(x)在(－∞，+∞)上是减函数．.……………..8分
(II)由1）可知
i) 当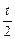<－1时，F(x)在x=－1处取得极小值－1－t，
在x=1处取得极大值3－t，若方程F(x)－m=0恰有两解，
此时m=－1－t或m=3－t．
ii) 当－1≤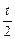<1，F(x)在x=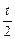处取值为，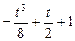
在x=1处取得极大值3－t，若方程F(x)－m=0恰有两解，
此时m=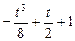或m=3－t．
iii) 当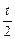≥1时，不存在这样的实数m，使得F(x)－m=0恰有两解．.……………..14