问题
填空题
若f(x)=x3+3ax2+3(a+2)x+1有极大值和极小值,则a的取值范围是__________。
答案
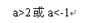
分析:先对函数进行求导,根据函数f(x)=x3+3ax2+3(a+2)x+1既有极大值又有极小值,可以得到导函数为0的方程有两个不等的实数根,从而有△>0,进而可解出a的范围.
解:f′(x)=3x2+6ax+3(a+2),
要使函数f(x)有极大值又有极小值,需f′(x)=3x2+6ax+3(a+2)=0有两个不等的实数根,
所以△=36a2-36(a+2)>0,解得a<-1或a>2.
