问题
解答题
已知函数f(x)=
(1)求函数f(x)的单调增区间; (2)当a=1时,函数h(x)=
|
答案
(1)∵f′(2)=4,f′(x)=x2+2ax+b,∴22+4a+b=4,解得b=-4a,
∴f′(x)=x2+2ax-4a,△=4a2+16a=4(a2+4a).
当△>0时,即a>0或a<-4时,x1,2=-a±
,函数f(x)的单调增区间:(-∞,-a-a2+4a
),(-a+a2+4a
,+∞).a2+4a
当△≤0时,即-4≤a≤4时,f′(x)≥0,函数f(x)的单调增区间:(-∞,+∞).
(2)∵h(2)=
=f(2)+ 1 3 g(2)
=1,即切点为(2,1).
+2 3 1 3 1
由h′(x)=
,得h′(2)=f′(x)g(x)-[f(x)+
]•g′(x)1 3 g2(x)
=1,f′(2)g(2)-[f(2)+
]•g′(2)1 3 g2(2)
所以,曲线h(x)在点(2,1)处的切线方程y=x-1.
当a=1时,b=-4.
由f(2)=
,∴2 3
+4a+2b+c=8 3
,得c=2,2 3
∴f(x)=
x3+x2-4x+2,f′(x)=x2+2x-4.1 3
当f′(x)=x2+2x-4=1,x2+2x-5=0,∴x=-1±
.6
当x=-1±
时,f(x)=6
±320 3
.6
而x=-1±
,y=x-1=-2±6
≠6
±320 3
.6
所以函数h(x)=
在点(2,h(2))处的切线不能与函数f(x)图象相切.f(x)+ 1 3 g(x)

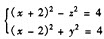 在yoz坐标面上的投影曲线方程为()。
在yoz坐标面上的投影曲线方程为()。