问题
选择题
用边长为48 cm的正方形铁皮做一个无盖的铁盒时,在铁皮的四角各截去一个面积相等的小正方形,然后把四边折起,就能焊接成铁盒,所做的铁盒容积最大时,在四角截去的正方形的边长为 ( )
A.12 cm.
B.16cm.
C.4 cm.
D.8 cm.
答案
答案:D
专题:应用题.
分析:根据题意先设小正方形边长为x,计算出铁盒体积的函数解析式,再利用导数研究此函数的单调性,进而求得此函数的最大值即可.
解答:解:设小正方形边长为x,铁盒体积为y.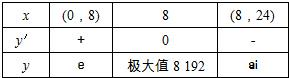
y=(48-2x)2?x=4x3-192x2+2304x.
y′=12x2-384x+2304=12(x-8)(x-24).
∵48-2x>0,
∴0<x<24.
∴x=8时,ymax=8192.
故选D.
点评:本小题主要考查函数模型的选择与应用,属于基础题.解决实际问题通常有四个步骤:(1)阅读理解,认真审题;(2)引进数学符号,建立数学模型;(3)利用数学的方法,得到数学结果;(4)转译成具体问题作出解答,其中关键是建立数学模型.
