问题
解答题
((本小题12分)
函数f(x)= 4x3+ax2+bx+5的图像在x=1处的切线方程为y=-12x;
(1)求函数f(x)的解析式;
(2)求函数f(x)在 [—3,1]上的最值。
答案
解:(1)f 1(x)= 12x2+2ax+b
∵y =f(x)在x=1处的切线方程为 y=-12x
∴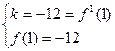 即
即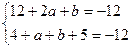
解得:a=-3  b=-18
b=-18
∴f(x)=4x3―3x2―18x+5
(2)∵f 1(x)= 12x2-6x-18=6(x+1)(2x-3)
令f 1(x)=0 解得:x=-1或x=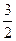
∴当x<-1或x>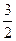 时,f 1(x)>0
时,f 1(x)>0
当-1<x<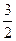 时, f 1(x)<0
时, f 1(x)<0
∵ x∈[-3,1] ∴在[-3,1]上无极小值,有极大值f(-1)=16
又∵f(-3)=-76 f(1)=-12
∴f(x)在[-3,1]上的最小值为-76,最大值为16。
