问题
填空题
| 将边长为2,一个内角为60°的菱形ABCD沿较短对角线BD折成四面体ABCD,点E,F分别为AC,BD的中点,则下列命题中正确的是______. ①EF∥AB;②EF⊥BD;③EF有最大值,无最小值;④当四面体ABCD的体积最大时,AC=
|
答案
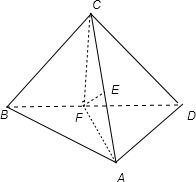
如图:由题意得,EF与AB是异面直线,故①不正确.
由等腰三角形的中线性质得 CF⊥BD,AF⊥BD,DB⊥面ACF,又EF?面ACF,
∴EF⊥BD,故②正确.
EF是等腰三角形FAC的底边上的中线,∴EF⊥AC,由于 FA=FC=
,斜边AC的长度不定,3
故 EF无最大值,也无最小值,故③不正确.
当四面体ABCD的体积最大时,因为等边△ABD的面积为定值,故面SBD⊥面ABD,CF为四面体的高,AC=
=CF2+FA2
=3+3
,故④正确.6
由DB⊥面ACF 得,DB⊥AC,又EF⊥AC,∴AC⊥面EBD,故⑤正确.
综上,②④⑤正确,
故答案为 ②④⑤.
