（1）a≥1时，在（-，+）是增函数；0<a<1时, f（x）在（－，x₂），（x₁，+）上是增函数；f（x）在（x₂，x₁）上是减函数；（2）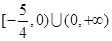

题目分析：（1）首先求出函数的导数，然后求出是或的解集即可.

（2）分类讨论在区间（1，2）上使成立的条件，并求出参数a的取值范围即可

试题解析：（1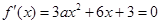），的判别式△=36（1-a）.

（i）若a≥1，则，且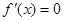当且仅当a=1，x=-1，故此时f（x）在R上是增函数.

（ii）由于a≠0，故当a<1时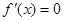，有两个根：，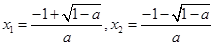

若0<a<1,则当x∈（－，x₂）或x∈（x₁，+）时，，故f（x）在（－，x₂），（x₁，+）上是增函数；

当x∈（x₂，x₁）时，，故f（x）在（x₂，x₁）上是减函数；

（2）当a>0，x>0时, ，所以当a>0时，f（x）在区间（1，2）是增函数.

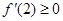若a<0时，f（x）在区间（1,2）是增函数当且仅当且，解得.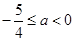

综上，a的取值范围是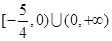.