问题
解答题
设函数f(x)＝axn(1－x)＋b(x＞0)，n为正整数，a，b为常数．曲线y＝f(x)在(1，f(1))处的切线方程为x＋y＝1.
(1)求a，b的值；
(2)求函数f(x)的最大值．
答案
(1) a＝1，b＝0. (2)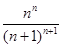 
(1)因为f(1)＝b，由点(1，b)在x＋y＝1上，可得1＋b＝1，即b＝0.
因为f′(x)＝anxn－1－a(n＋1)xn，所以f′(1)＝－a.
又因为切线x＋y＝1的斜率为－1，所以－a＝－1，即a＝1.故a＝1，b＝0.
(2)由(1)知，f(x)＝xn(1－x)＝xn－xn＋1，f′(x)＝(n＋1)xn－1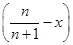
.
令f′(x)＝0，解得x＝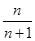
，在
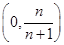上，f′(x)＞0，故f(x)单调递增；
而在
上，f′(x)＜0，故f(x)单调递减．
故f(x)在(0，＋∞)上的最大值为f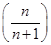
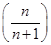＝n·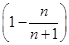
＝.
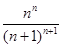