问题
解答题
在3000与8000之间，
（1）有多少个没有重复数字且能被5整除的奇数？
（2）有多少个没有重复数字的奇数？
答案
解：（1）若能被5整除且为奇数，则末位为5，只有1种可能，
首位可为3，4，6，7，共有4种可能，
其余两位共有
种可能，
由分步乘法计数原理知，共有1×4×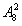
=224个。
（2）以首位是否选奇数分类：
第1类，首位选奇数3，5，7；
第1步，首位有3种选择；
第2步，末位有4种选择；
第3步，其余有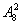
种选择，
共有
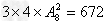个；
第2类，首位选4或6，
同理，此类共有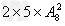
=560个；
由分类加法计数原理知，共有672+560=1232个。