问题
填空题
函数f(x)=x3-3ax+b(a>0)的极大值为6,极小值为2,则f(x)的单调递减区间是______.
答案
(-1,1)
令f′(x)=3x2-3a=0,得x=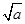 或-
或-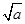 .
.
f(x),f′(x)随x的变化情况如下表:
| x | (-∞,-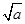 ) ) | -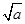 | (-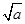 , ,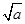 ) ) | 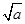 | (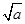 ,+∞) ,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | | 极大值 |  | 极小值 |  |
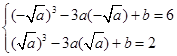 得
得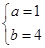 所以f(x)的单调递减区间是(-1,1).
所以f(x)的单调递减区间是(-1,1). 函数f(x)=x3-3ax+b(a>0)的极大值为6,极小值为2,则f(x)的单调递减区间是______.
(-1,1)
令f′(x)=3x2-3a=0,得x=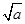 或-
或-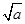 .
.
f(x),f′(x)随x的变化情况如下表:
| x | (-∞,-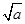 ) ) | -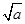 | (-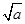 , ,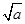 ) ) | 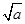 | (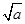 ,+∞) ,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | | 极大值 |  | 极小值 |  |
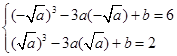 得
得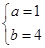 所以f(x)的单调递减区间是(-1,1).
所以f(x)的单调递减区间是(-1,1).