答案：D

题目分析：设F（x）="f" （x）g（x），当x＜0时，∵F′（x）=f′（x）g（x）+f （x）g′（x）＞0．∴F（x）在当x＜0时为增函数．

∵F（-x）="f" （-x）g （-x）="-f" （x）•g （x）=-F（x）．

故F（x）为（-∞，0）∪（0，+∞）上的奇函数．

∴F（x）在（0，∞）上亦为增函数．

已知f(－3)·g(－3)＝0，必有F（-3）=F（3）=0．

构造如图的F（x）的图象，

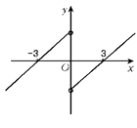
可知F（x）＜0的解集为x∈（-∞，-3）∪（0，3）．

点评：导数是一个新内容，也是高考的热点问题，要多注意复习．解决该试题的关键是先根据f’（x）g（x）+f（x）g’（x）＞0可确定[f（x）g（x）]'＞0，进而可得到f（x）g（x）在x＜0时递增。