问题
解答题
(2013•浙江)已知a∈R,函数f(x)=2x3﹣3(a+1)x2+6ax
(Ⅰ)若a=1,求曲线y=f(x)在点(2,f(2))处的切线方程;
(Ⅱ)若|a|>1,求f(x)在闭区间[0,|2a|]上的最小值.
答案
(1)y=6x﹣8
(2)f(x)在闭区间[0,|2a|]上的最小值为g(a)=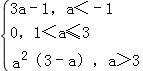 .
.
(Ⅰ)当a=1时,f′(x)=6x2﹣12x+6,所以f′(2)=6
∵f(2)=4,∴曲线y=f(x)在点(2,f(2))处的切线方程为y=6x﹣8;
(Ⅱ)记g(a)为f(x)在闭区间[0,|2a|]上的最小值.
f′(x)=6x2﹣6(a+1)x+6a=6(x﹣1)(x﹣a)
令f′(x)=0,得到x1=1,x2=a
当a>1时,
| x | 0 | (0,1) | 1 | (1,a) | a | (a,2a) | 2a |
| f′(x) | + | 0 | ﹣ | 0 | + | ||
| f(x) | 0 | 单调递增 | 极大值3a﹣1 | 单调递减 | 极小值 a2(3﹣a) | 单调递增 | 4a3 |
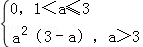 ;
;当a<﹣1时,
| X | 0 | (0,1) | 1 | (1,﹣2a) | ﹣2a |
| f′x) | ﹣ | 0 | + | ||
| f(x) | 0 | 单调递减 | 极小值3a﹣1 | 单调递增 | ﹣28a3﹣24a2 |
∴f(x)在闭区间[0,|2a|]上的最小值为g(a)=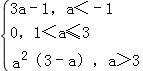 .
.
