问题
填空题
.若f(x)=x3+3ax2+3(a+2)x+1没有极值，则a的取值范围为 .
答案
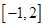
解：f′（x）=3x2+6ax+3a+6=3（x+a）2-3（a-2）（a+1）
当-1≤a≤2时，f′（x）＞0，所以函数单调递增，没有极值．
故答案为：[-1，2]
搜题请搜索小程序“爱下问搜题”
.若f(x)=x3+3ax2+3(a+2)x+1没有极值，则a的取值范围为 .
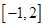
解：f′（x）=3x2+6ax+3a+6=3（x+a）2-3（a-2）（a+1）
当-1≤a≤2时，f′（x）＞0，所以函数单调递增，没有极值．
故答案为：[-1，2]
