问题
解答题
已知函数f(x)＝x2－(2a＋1)x＋alnx.
（1）当a＝1时，求函数f(x)的单调增区间；
（2）求函数f(x)在区间[1，e]上的最小值；
答案
（1）(0，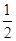
)，(1，＋∞) （2）a(lna－a－1)
本试题主要考查了导数在研究函数中的运用。
解：(1)当a＝1时，f(x)＝x2－3x＋lnx，定义域为(0，＋∞)，
f′(x)＝2x－3＋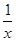
＝
＝
.
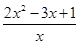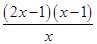令f′(x)＝0，得x＝1或x＝.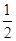
| x | (0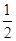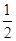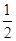，) | | (，1) | 1 | (1，＋∞) |
| f′(x) | ＋ | 0 | － | 0 | ＋ |
| f(x) |  | 极大值 |  | 极小值 |  |
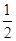)，(1，＋∞)． (2)f′(x)＝2x－(2a＋1)＋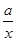
＝
＝
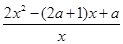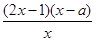，令f′(x)＝0，得x＝a或x＝.
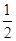当a≤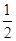时，f(x)在[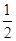，＋∞)上单调增，所以f(x)在区间[1，e]上单调增；
当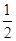<a≤1时，f(x)在(0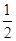，]，[a，＋∞)上单调增，所以f(x)在区间[1，e]上单调增．
综上，当a≤1时，f(x)min＝f(1)＝－2a；
当1<a<e时，
| x | (1，a) | a | (a，e) |
| f′(x) | － | 0 | ＋ |
| f(x) |  | a(lna－a－1) | |