问题
解答题
已知二次函数y=ax2+bx+c(a≠0)的图象经过O(0,0),M(1,1)和N(n,0)
(n≠0)三点.
(1)若该函数图象顶点恰为M点,写出此时n的值及y的最大值;
(2)当n=-2时,确定这个二次函数的解析式,并判断此时y是否有最大值;
(3)由(1)、(2)可知,n的取值变化,会影响该函数图象的开口方向.请求出n满足什么条件时,y有最小值.
答案
(1)由二次函数图象的对称性可知n=2;
y的最大值为1.
(2)由题意得:
,a+b=1 4a-2b=0
解这个方程组得:
;a= 1 3 b= 2 3
故这个二次函数的解析式为y=
x2+1 3
x;2 3
∵
>0,1 3
∴y没有最大值;
(3)由题意得:
,a+b=1 an2+bn=0
整理得:an2+(1-a)n=0,即n(an+1-a)=0;(8分)
∵n≠0,
∴an+1-a=0;
故(1-n)a=1,而n≠1;
若y有最小值,则需a>0,∴1-n>0,即n<1;
∴n<1且n≠0时,y有最小值.

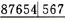 缺失,拟行可摘局部义齿修复,但患者对塑料严重过敏,余牙及缺牙间隙正常
缺失,拟行可摘局部义齿修复,但患者对塑料严重过敏,余牙及缺牙间隙正常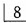 设计正型卡环,其固位力多少为宜()
设计正型卡环,其固位力多少为宜()