问题
解答题
设函数f(x)=x(x-1)(x-a),(a>1)。
(1)求导数f′(x),并证明f(x)有两个不同的极值点x1,x2;
(2)若不等式f(x1)+f(x2)≤0成立,求a的取值范围。
答案
解:
令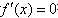 得方程
得方程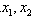
因
故方程有两个不同实根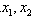
不妨设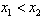
由 可判定f′(x)的符号如下:
可判定f′(x)的符号如下:
当 时,f'(x)>0
时,f'(x)>0
当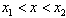 时,
时,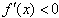
当 时,
时,
因此 是极大值点,
是极大值点,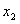 是极小值点。
是极小值点。
(2)因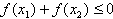 ,故得不等式
,故得不等式

即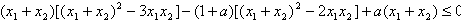
又由(1)知
代入前面不等式,两边除以(1+a),并化简得
解不等式得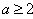 或
或 (舍去)
(舍去)
因此,当 时,不等式
时,不等式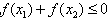 成立。
成立。
