问题
解答题
已知函数f(x)＝x3－3ax2＋2bx在点x＝1处有极小值－1.
(1)求a、b；
(2)求f(x)的单调区间．
答案
（1）
（2）在区间
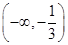和(1，＋∞)上，函数f(x)为增函数；
在区间
上，函数f(x)为减函数．
(1)由已知，可得f(1)＝1－3a＋2b＝－1，①又f′(x)＝3x2－6ax＋2b，
∴f′(1)＝3－6a＋2b＝0.②由①②解得
(2)由(1)得函数的解析式为f(x)＝x3－x2－x.
由此得f′(x)＝3x2－2x－1.
根据二次函数的性质，
当x<－
或x>1时，f′(x)>0；
当－<x<1时，f′(x)<0.
因此，在区间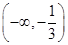和(1，＋∞)上，函数f(x)为增函数；
在区间上，函数f(x)为减函数．