问题
解答题
已知函数f(x)＝4x3＋3tx2－6t2x＋t－1，x∈R，其
中t∈R.
①当t＝1时，求曲线y＝f(x)在点(0，f(0))处的切线方程；
②当t≠0时，求f(x)的单调区间．
答案
①6x＋y＝0②在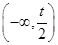
上递增，
上递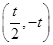减，(－t，＋∞)上递增．
①t＝1时，f(x)＝4x3＋3x2－6x，f′(x)＝12x2＋6x－6，f′(0)＝－6，又f(0)＝0.
∴曲线y＝f(x)在点(0，f(0))处的切线方程为y－0＝－6(x－0)，即6x＋y＝0.
②t≠0时，f′(x)＝12x2＋6tx－6t2＝6(2x2＋tx－t2)＝6(x＋t)(2x－t)．若t>0，则由f′(x)>0得x<－t或x>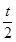
，f′(x)<0得－t<x<，
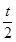∴f(x)在(－∞，－t)上递增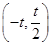，在
上递减．在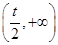
上递增，
若t<0，则由f′(x)>0得x<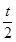或x>－t，由f′(x)<0得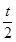<x<－t.
∴f(x)在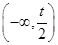上递增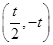，上递减，(－t，＋∞)上递增．